Loudness: Sonic (i.e. perceptual) attribute of sound waves, related mainly to intensity.
In general, high intensity values result in 'loud' sounds while low intensity values result in 'quiet' sounds.

In perceptual terms, loudness is a manifestation of how the auditory system
       a) represents sound wave intensity &
       b) makes intensity comparisons among signals across frequency and time. 
 
In physiological terms, loudness is a manifestation of the total activity on the basilar membrane.
 
In neurological terms, loudness is a manifestation of the total activity on the auditory nerve. 

Stevens's Power Law

Loudness L is proportional to some power of Intensity I.
[L = kI^a,  where a =~ 0.2-0.3, for frequencies >~200Hz and for a large range of intensities.]

Multiplication in the physical variable of intensity corresponds to addition in the perceptual variable of loudness. Consequently, as intensity rises, an increasingly larger amount of intensity (i.e. energy-flow per unity area) is needed to produce the same loudness increase.

 

Key Facts / Reminders:

1. Sound Intensity Level (SIL) is a logarithmic measure, devised because
   a) perceived intensity (i.e. loudness) is related approximately logarithmically to the physical magnitude of intensity &
   b) logarithmic scales can represent very large ranges of values more effectively, matching the dynamic compression capacity of the hearing mechanism (i.e. via the outer hair-cell response, in the organ of Corti, within the cochlea).
    
      Examples:
    
       Increasing the intensity by a factor of 2 corresponds to a 3dB SIL increase; by a factor of 4 to a 6dB SIL increase, etc.
       Increasing intensity by a factor of 10 corresponds to a 10dB SIL increase and the perception of ~twice as loud;
       Increasing intensity by a factor of 100 corresponds to a 20dB SIL increase and the perception of 4-times as loud; etc.
    

2. Intensity I (in w/m²) and Sound Intensity Level SIL (in dB) are alternative but fully equivalent physical measures.
   They simply use different scales. 
   I : absolute measure, using a linear scale; unit 1w/m².  
   SIL : relative measure (ratio of a given intensity over a reference intensity value), using a logarithmic scale; unit 1dB. 
    
   Every Intensity value I corresponds to a single Sound Intensity Level SIL value, following a mathematical transformation. In this transformation, the assigned SIL value reflects how a given I value compares to a reference I value that corresponds to a barely audible sound. 
   If Intensity = I w/m² then Sound Intensity Level is SIL = 10*log₁₀ I/10^-12 in dB,  where  10^-12w/m² is the intensity of a barely audible sound.
    

3. Intensity and SIL are both measures of the same physical variable: energy-flow per unit area.
    

4. Sound Pressure Level (SPL) relates to pressure analogously to how SIL relates to Intensity. Like SIL, SPL is logarithmic.
     

5. Neither Intensity, nor SIL, nor pressure, nor SPL measure loudness, which is a perceptual variable and depends on several physical/physiological variables beyond Intensity, SIL, pressure, or SPL.

Dynamic Range of the ear: A range of Intensities/SILs that the auditory system can process effectively,  bounded by lower and upper limits.

Dynamic range of functional and safe hearing: from   ~10^-12w/m² or 0dB  (at 1000Hz)   to ~1w/m² or 120dB (at all frequencies).

SILs below 0dB are inaudible (to most people at most frequencies)
SILs above 120dB are damaging to the ear, more so the longer the exposure and the steeper the attack.
 

The lower limit of the ear's dynamic range (or absolute threshold) is usually explored and presented in the form of audiograms, obtained in loudness magnitude matching experiments (see the discussion on Phons, below).

Audiograms: graphs plotting the absolute threshold (i.e. lowest audible level) of sinusoidal signals as a function of frequency. See, for example, the lowest curve (bolded) in the figure, below; (FIG. 6.1., from Plack, C.J., 2005. The Sense of Hearing. New York, NY: Psychology Press/Taylor & Francis).

Observations:

a) the lowest audible intensity is different for different frequencies; this means that different frequencies become barely audible at different SILs/SPLs &
b) for different frequencies to sound equally loud, their SIL (or SPL) has to be different.

More details on these curves, called equal loudness curves/contours, in the next section.
 

The upper limit of the ear's dynamic range may be defined in several ways:

a) Intensity level eliciting an unpleasant, even painful sensation, which may cause physiological damage (~120dB)
 
b) Intensity level beyond which telling level differences apart becomes very difficult.
This ability starts deteriorating at levels ~>100dB, but remains possible even at levels >120dB.

The dynamic range of the ear is therefore ~120dB in the mid-frequency region most relevant to speech signals (1000-6000Hz; increasing to ~130dB within the 2000-5000Hz range) and decreases at lower and higher frequencies.

This dependence of our hearing mechanism's dynamic range on frequency is due to the fact that, at frequencies outside the 1-6kHz range, the lower limit increases while the upper limit stays relatively fixed at ~120dB.

Just Noticeable Difference (JND) for loudness: ~1dB  -  for pure (sine) tones, middle frequencies and 'regular' background noise.

Weber's law (for Just Noticeable Difference)

According to Weber's (fraction) law (after 19th century German physician, Ernst H. Weber), the smallest perceivable physical change in a stimulus is proportional to the starting level of the physical stimulus (referred to as pedestal), so that their ratio remains constant.
Therefore, for pedestal intensity of I and intensity change of ΔI , Weber's law says that ΔI / I = constant.

In practical terms:
The higher the SIL of a signal, the more dB must be added/removed for listeners to perceive the SIL change as a loudness change. [Experiments have shown that our ability to discriminate intensity levels actually degrades less than predicted by Weber's "law," an observation referred to as "Weber law 's near miss"]

Loudness & Frequency /  Loudness Scales

 

Effects of Frequency on Loudness 

The equal loudness contours or ELCs (Fig. 6.1, above and figures below) illustrate that loudness does not only depend on intensity; it also depends on frequency and does so differently at different starting intensities. 
More specifically, the equal loudness contours demonstrate that

i) the sensitivity of the ear drops significantly at low (approx. <350Hz) and high (approx. >15kHz) frequencies and

ii) loudness depends on SIL non-linearly (i.e. the dependence of loudness on frequency is not the same at all SILs), as indicated by the fact that the shape of the curves changes (becomes flatter) as we increase intensity levels.

The figures, below, are based on a series of 1930s experiments, while Fig. 6.1, above, is based on 2003 revisions of and additions to these data. The main difference between the two graphs is for frequencies below 1000Hz (latest revision).

Sample Observations

i) A pure tone with SIL = 60dB will sound moderately loud at 1000Hz but will be barely audible at 50 Hz.
 
ii) At high frequencies (approx. between 6000 and 15000Hz), the drop in sensitivity is not as dramatic as it is at low frequencies (approx. below 350Hz).

As previously noted, our increased sensitivity to frequencies in the range ~1000Hz-6000Hz may have some evolutionary significance, since speech sounds have most of their energy within this range (see a discussion on formant frequencies for different vowels).

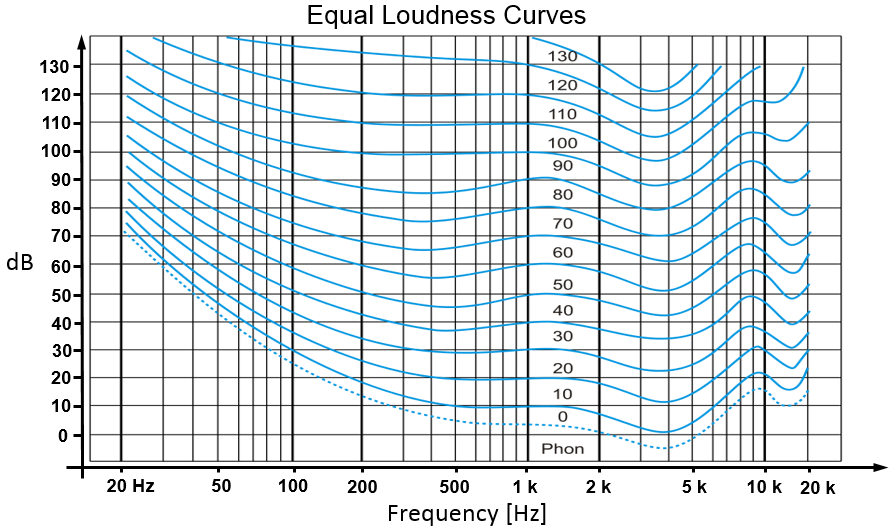Equal loudness contours/curves for pure tones (after Fletcher and Munson, 1933)

 

For example (see above):
If a 1000Hz tone is played at 40dB, then a 100Hz tone has to be played at 52dB in order to sound equally loud.
 

Watch this frequency-sweep video to experience the impact of frequency on loudness at a fixed SIL.

[Optional: Scientific paper exploring Equal Loudness Contours in detail.]

 
LOUDNESS SCALES
Loudness Level Unit vs. Loudness Unit
 

Loudness Level Unit

The loudness level unit is called phon.
Loudness level in phons and SIL in dBs are equivalent only at 1000Hz; intensity and loudness do not map isomorphically (i.e. there is no one-to-one correspondence between them): SIL only depends on Intensity while loudness depends on both, intensity and frequency. 

The loudness level, in phons, of a given SIL at a given frequency is equal to the SIL of an equally loud tone at 1000Hz.
Consequently, frequency & SIL pairs that fall on the same curve in the figures, above:
a) sound equally loud, b) are equal in loudness phon units, and c) are most likely unequal in SIL dB units. 

For example, all 4 freq/SIL pairs, below, sound equally loud, with loudness level of 10 Phon:
100Hz at ~30dB SIL    -    200Hz at ~20dB SIL    -    1000Hz at ~10dB SIL    -    3000Hz at ~0dB
This loudness equivalence, in spite of the SIL difference, is expressed in that all four pairs lay on/near the 10 phon contour line of the ELCs.

Similarly to the lower limit of the ear's dynamic range, the phon loudness level unit is determined based on loudness magnitude matching experiments.

Loudness magnitude matching: Listeners are asked to adjust the SIL of a tone with a given frequency so that it matches in loudness the loudness of a 1000Hz tone with a given SIL. 

For a good summary of phons see also here.

Weighting Curves (spectral filters)

A variety of weighting curves have been devised (A, B, C, and D) to assist analog/digital recording, measuring, and broadcast equipment (with assumed flat, or near flat response) in simulating the ear's frequency-dependent response to intensity. These curves are mainly used in noise measurement, loudness calculations, and hearing evaluations and NOT in sound mixing and mastering.

Each type of curve captures best the ear's response at a different input-level range. 

A-weighting mimics hearing response at low levels (~40phons).
 
B-weighting mimics hearing response at medium levels (~70phons)
 
C-weighting mimics hearing response at high levels (~>100phons)
 
D-weighting is similar to the B-weighting curve but with a ~10dB boost at the 2-6kHz range, meant to represent loudness perception of loud level random noise (e.g. aircraft).

The A-weighting curve is the one most commonly used in environmental noise assessments. 
The C-weighting curve is used specifically for low-frequency noise assessment.
The B- and D-weighting curves are rarely used and have now been removed from
the international standard for loudness measurement.

For more details see the opening paragraphs of the articles on Weighting Curves in Wikipedia and the Lindos Electronics page (UK).
Bookmark these resources for future reference. Proper use of weighting curves is necessary in most broadcast a/v projects, which require adherence with loudness standards.

Loudness Unit

Loudness magnitude matching experiments reveal the dependence of loudness on frequency but do not support the construction of a linear loudness scale. 
Such a scale can be derived by loudness magnitude estimation and production experiments.

Loudness magnitude estimation: Listeners are asked to compare the loudness of two tones and determine how much louder/quieter the 2nd tone is relative to the 1st.
Loudness magnitude production: Listeners are asked to adjust the SIL of a tone so that it becomes, say, twice as loud as another tone with known and fixed SIL.

Loudness magnitude estimation & production experiments use as standard reference a 1000Hz tone at 40dB SIL. The sound loudness level (SLL) of any tone is then described in relation to this reference standard, whose loudness is defined as:

1 Sone (Loudness unit):
Loudness of a 1000Hz tone at SIL/SPL of 40dB.

The advantage of the sone scale is that it is based on loudness units that are proportional to loudness and can be manipulated arithmetically (e.g. two sones sound twice as loud as one sone; three sones sound three times as loud, etc.). 

The sone scale is more valid than the dB or the phon scales, because it was derived based on both sine and complex tone loudness judgments. Nonetheless, most discussions on loudness continue to use dBs and phons because of the complex transformations necessary to work with sones.

Graphical depiction of the relationship between phons and sones
dB-Phons-Sones converter: http://www.sengpielaudio.com/calculatorSonephon.htm

Loudness and Spectrum (bandwidth)

Effects of Spectrum (bandwidth) on Loudness

For complex tones, loudness also depends on spectrum (i.e. on the way energy is distributed among the complex tone's components).

Suppose that two complex tones have the same SIL (in dB) but they have different spectra. The complex tone with more 'spread-out' spectrum (i.e. with components spreading across more critical bands) will sound louder than the one with a less 'spread-out' spectrum (i.e. with components spreading across fewer critical bands).
See the figure to the right (source).

More specifically (see the figures, below):
_ Regardless of SIL, as long as the bandwidth of a complex signal remains within a given number of critical bands relative to the spectrum's center frequency, changing a signal's spectral bandwidth, while keeping the overall SIL fixed, will have no effect on loudness (refresh your memory on critical bands). 
_ For moderate to high SILs, if the spectral bandwidth is increased (decreased) to excite a larger (smaller) number of critical bands, then the loudness will increase (decrease).
_ As SIL decreases, so does the effect of spectral bandwidth changes on loudness.

[ If all frequencies components in a complex tone are within a single critical band, the total loudness can be approximated by the sum of all loudness levels per component.
If the frequency components are spread over multiple critical bands, the total loudness is larger and can be approximated by the sum of the sound loudness levels per critical band. ]

 
The phenomenon of simultaneous masking (perceptual erasure of one sound by a more intense/loud sound - refresh your memory) is an additional example of the dependence of loudness on spectral distribution. The disturbance pattern on the basilar membrane is wider and the response is faster for high intensity sounds than for low intensity sounds, facilitating masking. In addition, due to the general asymmetry in the disturbance pattern of the basilar membrane, strong low-frequency sounds will mask weak high-frequency sounds more efficiently than the other way around.

The following two dependencies play an important role in audio data compression algorithm design, by helping determine what portions of a signal can be removed (to accomplish data reduction) without noticeably changing the sound of the original signal.
_ Dependence of loudness on frequency & spectral bandwidth.
_ Dependence of masking on frequency & level differences.

Loudness and Duration

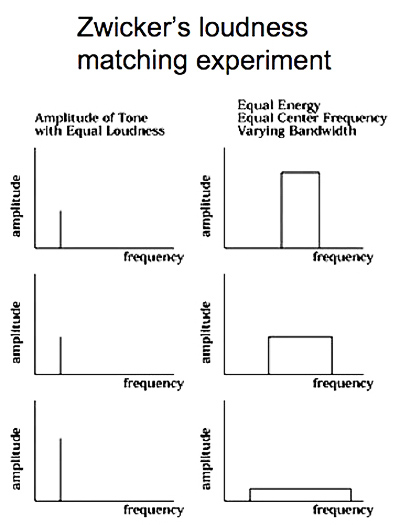Effects of Duration on Loudness

The auditory system responds to abrupt intensity changes with a "rise time" of  ~200ms and a "decay time" of ~50ms. The indicated "decay time" may explain why tones with frequency >20Hz (<50ms period) are perceived as a single tone with identifiable pitch rather than individual pulses or why amplitude fluctuation rates above 20Hz may be perceived as "roughness" or combination tones rather than as loudness fluctuations or "beats." 
 
In general, for durations up to ~200ms, (~400ms for broadband signals) the longer the signal the louder it appears. In other words, the ear appears to average sound energy over ~200ms for narrow band signals and ~400ms for broadband signals. Within this duration range, tenfold increase in duration corresponds to 10 Phons increase in loudness.

For longer durations (>1-2 secs), no consistently loudness changes have been recorded with increase in duration.
Much longer durations do impact loudness, as well, but for different reasons (see the section on Adaptation/Fatigue, further below).

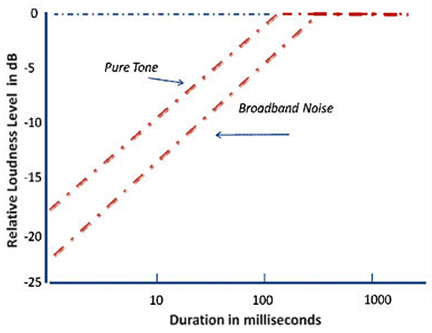Loudness and time-delay among successively presented stimuli:

Presentation delay (time distance) between signal onsets also influences loudness, but not in a significant way. You can deduce this influence from your understanding of forward and backward masking. We will return to this issue during our discussion on sound quality (i.e. timbre).

SUMMARY
(Loudness & Intensity / Frequency / Spectrum / Duration)

Loudness & Intensity

All else (i.e. frequency, spectrum, and duration) being equal:

Increasing intensity increases loudness, logarithmically:
As Intensity rises, an increasingly larger amount of intensity is needed to produce the same increase in loudness. Linear Intensity scales (I, in w/m²) are therefore converted into logarithmic Sound Intensity Level scales (SIL, in dB) that are constructed relative to the lowest audible intensity.
   [Analogously, linear pressure (P, in Pascals) scales are converted to Sound Pressure Level (SPL, in dB) scales].

Lowest audible intensity: I₀ = 10^-12 w/m²; SIL = 0 dB.
Highest safely audible intensity: = 1 w/m²; SIL = 120dB

Average dynamic range of human hearing: 120dB (on average, and at 1000Hz; dynamic range changes with frequency)

Just Noticeable Difference (JND) is the minimum SIL change that can be perceived as loudness change:

~1dB at moderate levels and middle frequencies, increasing:
         _at starting levels > 95-100dB
         _for frequencies above middle frequencies; even more, for frequencies below middle frequencies.

Loudness & Frequency

All else (i.e. intensity, spectrum, and duration) being equal:

Middle frequencies (1-6kHz) have lower threshold and larger dynamic range than higher frequencies, which have lower threshold and larger dynamic range than lower frequencies. Expressed differently: Sensitivity and dynamic range are lowest/smallest at low frequencies, higher/larger at high frequencies, and highest/largest at middle frequencies.

At low SILs, the ear's response to level depends strongly on frequency (i.e. at low SILs, signals of the same level will have significant loudness differences depending on frequency). The same SIL sounds quietest at low frequencies, louder at high frequencies and loudest at middle frequencies.
As SIL increases this effect decreases and the ear's frequency response becomes increasingly flat (i.e. same SILs sound almost equally loud regardless of frequency).

The Equal Loudness Contours describe the above relationships (i.e. dependence of loudness on frequency at different SILs).
     Frequency/SIL pairs on a given line sound equally loud, as loud as the 1000Hz/SIL pair on the same line.

The Loudness Level Unit is called phon. It captures the dependence of loudness on both SIL and frequency.
     At 1000Hz, Loudness Level (in phons) and Sound Intensity Level/SIL (in dB) are identical.
     Different frequencies that sound equally loud have the same loudness level (in phons) but likely different SILs (in dB).
 
The Loudness Unit is called sone. It is proportional to perceived loudness level and can be manipulated arithmetically.
     Loudness of 1 sone is defined as the loudness of a 40dB 1000Hz tone.

Loudness & Spectrum

For complex tones, and all else being equal (i.e. center frequency, overall intensity, and duration):

The wider the spectrum (i.e. the larger the spectral bandwidth  /  the larger the frequency range occupied by the spectrum  /  the more spread-out on the graph the frequency components), the louder the sound. assuming that:

a) the wider spectrum corresponds to more critical bandwidths (in the ear) than the narrower spectrum
b) the overall SIL is >~30dB.

Conversely, the narrower the spectrum the more likely for multiple frequency components to fall within the same critical band and the lower the loudness.
In addition, the more frequency components within the same critical bandwidth
     a) the more likely for interference artifacts (beating / roughness) and masking to occur and
     b) the less the clarity.
Rule of thumb: the larger the bandwidth occupied by a musical arrangement the louder and the clearer the sound.
So, in this case you can have it both ways: louder and clearer!

Loudness and Duration

All else (i.e. center frequency, overall level, and spectral bandwidth) being equal:

For durations up to 200ms for narrow-band signals and up to 400ms for broadband signals, the longer the signal the louder it appears.
Much longer durations impact loudness differently, as described in the following section (Adaptation/Fatigue)

 

Links to Save for Future Reference

The Loudness War (Wikipedia)
 
How Loud Should You Mix? (Sweetwater.com)
 
Four Essential Mastering Level Tips (Waves.com)
 
Mixing Sound for Film (The BeachHouse Studios)
 
How to Produce a Powerful Drop for Your Song (MasteringTheMix.com)
 
What Data Compression Does to Your Music (SoundOnSound.com)
 
Audio Measurement Articles (Lindos.uk)
 
mp3s and the Degradation of Listening (Pantelis Vassilakis - DePaul University Blog)
 

Hearing Loss & Conservation
 

 

Hearing loss is a common condition caused by noise, aging, disease, and heredity.

The basilar membrane gets stiffer with age, resulting in loss of sensitivity especially for high frequencies, (condition called Presbycusis). In general, age-related hearing loss impacts men more than women.

Hearing loss due to environmental and behavioral factors (as opposed to age and heredity) is both more significant and easier preventable.

Exposure to high intensity sounds can result in temporary damage (TTS or temporary threshold shift: temporary reduction in sensitivity), manifested as reduced sensitivity (inability to hear low level sounds) and ear ringing.
Repeated, prolonged exposure to high intensity sounds can cause permanent hearing loss due to hair cell damage (see below and to the left)

 .
Healthy and damaged hair cells (after Curtis, 1979)

Unfortunately:
Noise- and music-induced hearing loss is cumulative, irreversible, and painless (no pain warnings).
Fortunately:
Noise- and music-induced hearing loss is ~100% preventable.

Music-induced hearing loss (MIHL) is caused by exposure to music at levels >85 dB (analogous to the sound of heavy city traffic) for prolonged periods of time.
The leading cause of MIHL is the use of personal listening devices (e.g. Pienkowski, 2021). More specifically, the greatest risk is for personal listening > 1 hour daily > 50% volume for > 5 years (e.g. Fink & Mayes, 2021).

For every doubling of listening time the safe level drops by 3dB (can you guess why? see the image to the right).

Our understanding of equal loudness contours and otoacoustic emissions has contributed to the development of music listening hardware and software that are (or, claim to be) able to adjust to each listener's level of hearing health.

 

Sample Products. (this in not an endorsement; items listed for illustration purposes):

https://www.weareeven.com/
https://www.nuraphone.com/
https://avantree.com/

Hearing Conservation Resources for Future Reference

How to Save your Hearing On Tour   [ TourReady, 2018 ]

Music-Induced Hearing Loss   [ Hearing Health Foundation ]   Full article: Berg, A.L. et al., 2019.

Preventing Music-Induced Hearing Loss (Chesky, K., 2008)

1st International Conference on Music-Induced Hearing Disorders, organized by the Audio Engineering Society (Chicago, IL, 2012 - Columbia College Chicago). The conference meets every two years.